The Critical-Section Problem

To guard against the race condition previously discussed, we need to ensure that only one process at a time can be manipulating the variable count. To make such a guarantee, we require that the processes be synchronized in some way.

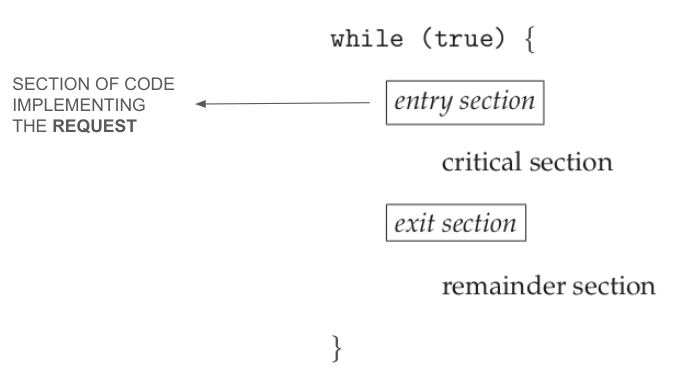
Consider a system consisting of n processes {P0, P1, ..., Pn-1}, each having a segment of code called critical section, in which the process may be accessing and updating data that is shared with at least one other process.

note

The important feature is that no two processes are executing in their critical sections at the same time.

Each process must request permission to enter its critical section.

Requirements

A solution to the critical-section problem must satisfy the following three requirements:

1. Mutual exclusion: If process Pi is executing in its critical section, then no other processes can be executing in their critical sections.
2. Progress: If no process is executing in its critical section, but there are processes that actively wish to enter their critical sections, then there is a guarantee that eventually some process will be selected (i.e. no process can be blocked forever).
3. Bounded waiting: There exists a bound, or limit, on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted.

Peterson's solution

This is a classic software-based solution to the critical-section problem. Because of the way modern computer architectures perform basic machine-language isntructions, there are no guarantees that Peterson's solution will work correctly on such architectures.

However, it's important to be studied because it provides a good algorithmic description that addresses the requirements.

Peterson's solution is restricted to two processes, P0 and P1, or for convenience, Pi and Pj with j = 1 - i.

The two processes share two data items:

// whose turn it is to enter its critical section
// turn == i => Pi is allowed to execute in its critical section
int turn;

// indicates if a process is ready to enter
// flag[i] = true => Pi is ready to enter its critical section
boolean flag[2];

Let's describe the algorithm:

petersons_solution.c

// Pi POV
while(true) {
    // I (Pi) am ready to enter my critical section
    flag[i] = true;

    // if Pj wishes to enter the cs, it can do so
    turn = j;

    // if both want to enter at the same time
    // turn will be set to both i and j at the same time
    // only one will last, the other will be overwritten
    // the eventual value determines which is allowed to enter first

    // if Pj wished to enter and is really his turn,
    // then I have nothing to do
    while (flag[j] && turn == j)
        ;

    /* critical section */

    // I don't want to enter my cs anymore
    flag[i] = false;

    /* remainder section */
}

Hardware Instructions

Many modern computer systems provide special hardware instructions that allow us either to test and modify the content of a word or to swap the contents of two words atomically - that is, as one uninterruptible unit.

These special instructions will help us solve the critical-section problem in a relatively simple mnner.

test_and_set()

The important characteristic of test_and_set() is that it is executed atomically.

boolean test_and_set(boolean *target) {
    boolean rv = *target;
    *target = true;

    return rv;
}

We can implement mutual exclusion by declaring a boolean variable lock = false.

mutex.c

// Pi POV
do {
    // if the lock is true, then someone else is in their cs
    // if it's false, then I can enter my cs and I set it true
    while (test_and_set(&lock))
        ;

    /* critical section */

    lock = false;

    /* remainder section */
} while (true);

compare_and_swap()

The CAS instruction operates on two words atomically, but uses a different mechanism that is based on swapping the content of two words.

int compare_and_swap(int *value, int expected, int new_value) {
    int temp = *value;

    if (*value == expected)
        *value = new_value;

    return temp;
}

mutex.c

while (true) {
    // Pi POV

    // if the lock is false as I expect, set it true
    // if it's true, then someone else is in their cs
    while (compare_and_swap(&lock, 0, 1) != 0)
        ;

    /* critical section */

    // another process can enter its cs
    lock = 0;

    /* remainder section */
}

danger

This algorithm does not satisfy the bounded-waiting requirement!

Check the book for a solution that solves the issue.